BFF is the name of the problem C in Google Code Jam 2016, Round 1A. The summarized problem statement is as follows:

Every kid in your class has a single best friend forever (BFF).
You want to form the largest possible circle of kids such that each kid in the circle is sitting directly next to their BFF, either to the left or to the right.
Give a line that contains N integers F1, F2, ..., FN, where Fi is the student ID number of the BFF of the kid with student ID i, find the greatest number of kids that can be in the circle.

I’m never a strong sport programmer. I’d like to approach to the problem more methodically. While the first three example test cases provided in the problem statement is pretty straight forward, the last example 7 8 10 10 9 2 9 6 3 3 is not so. Such number chains look like graphs or linked-lists and I would first try to plot them out:

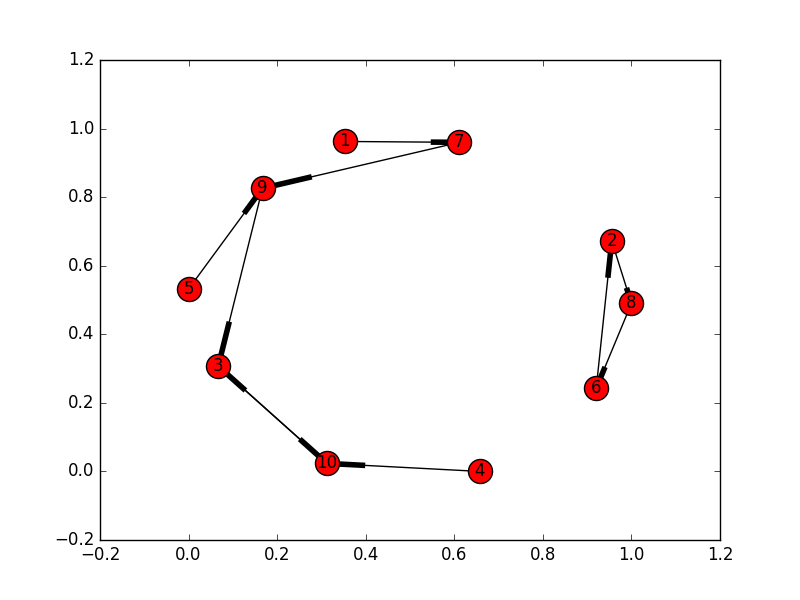
I initially thought that problem C is some dynamic programming problem (base case N=2) and tried to think in that direction. After looking at the graph plot for the last example (shown above), it is apparent to me that is not the case and I actually need some graph algorithm. The above plot also gives me some key observations to solve the problem:

1. Each cycle in the directed graph is a candidate for the solution circle.
2. If the kids form a cycle with length >= 3, then there is no way to insert another kid into that cycle to form a circle that satisfies the requirements.
   • In the example above, for the cycle 2->8->6->2, if there is a kid that is BFF to (i.e., a node pointing to) any one of them, we cannot create a larger circle to include that kid.
   • The cycle is a candidate for solution itself. Some cycles can get really large.
3. If the kids form a cycle with length == 2 (called “mutual BFFs” in my code), then you can keep chaining kids who are friends of friends to those kids to form a “path”. You can create a circle from one or more “paths”.
   • In the example above, for the cycle 3-10, we can chain friends of friends 1->7->9->3 and 10<-4 to form a longer chain 1-7-9-3-10-4. This path is another solution candidate.
   • After comparing length with the other candidate (cycle 2->8->6->2), the “path” is the solution circle for this particular example.

Based on those observations, the solution is pretty “simple”:

1. From the list of BFFs, construct a directed graph.
2. Find all the simple cycles in the directed graph. <- I lied, this is not simple.
3. Initialize max_length = -1. For each simple cycle:
   1. If cycle length is greater than 2, it is a candidate. Compare its length and update max_length if needed.
   2. If cycle length is equal to 2.
      1. Find the longest friends of friends chain that is connected to either kid in this cycle.
      2. Find the path length, add to path_sum, and update max_length if needed.

Constructing the directed graph and finding cycles in step 2 is not trivial but can be made easy using networkx module, as shown below (together with plotting using matlplotlib).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

import matplotlib.pyplot as plt
import networkx as nx

class Bff(object):
    """
    https://code.google.com/codejam/contest/4304486/dashboard#s=p2
    """
    def __init__(self, filename):
        """ Initialize with the given filename.

        :param filename: input file path
        :return:
        """
        self._filename = filename
        pass

    def draw(self, input):
        """ Draw the string that represents the bff network.

        The input string contains N integers F1, F2, ..., FN, 
        where Fi is the student ID number of the BFF
        of the kid with student ID i.

        :param input: the string that represents the bff network.
        :return:
        """
        # Construct the directed graph
        bffs = [int(e.strip()) for e in input.split(' ')]
        nodes = [i+1 for i in xrange(len(bffs))]
        gr = nx.DiGraph()
        gr.add_nodes_from(nodes)
        gr.add_edges_from([e for e in zip(nodes, bffs)])

        # nx.simple_cycles(gr)
        nx.draw_networkx(gr)
        plt.savefig(self._filename)

def main():
    plot = Bff("bff.png")
    # plot.draw("2 1 6 3 8 4 6 5")
    plot.draw("6 1 6 5 4 1 5 10 3 7")
    pass

Disclaimer: I know my solution is probably not accepted in Code Jam for using external library, and that is fine :D. It is not like I can implement Johnson’s algorithm for finding cycles within two hours. My solution is to check if my thinking is correct.

Note that one mistake we might make is to treat each “path” (found from cycles of length 2) as a solution candidate instead of combining them into a candidate (Note “one or more” in observation 3). The reason is that all the “paths” can be chained together to form a larger cycle (see graph below). My first solution was rejected for Small Input dataset due to this mistake. Again, by plotting test cases in the Small dataset, the following test case would came up and makes me realize my mistake:

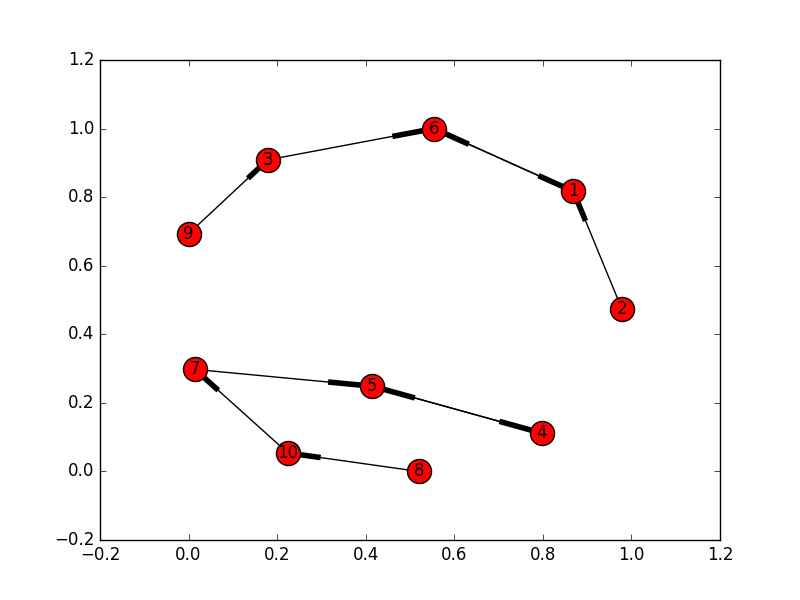
Some morals of the story:

• Plotting helps. Without looking at the graphs, I would wander into the wrong direction, looking for a DP solution.
• In real-world problem solving, you don’t need to solve the problem in two hours. Even better, you don’t need to re-invent the wheel. Therefore, it is better to take steps methodically to arrive at a scalable solution (i.e., plotting, using libraries, testing if needed).